CS and mathematics

문제 해석

자연수 \(x_1..x_n\)이 있고, 모두 서로 다르다는 사실만 알고 있다. 두 인덱스 \(i, j\)를 고르면 \(\min(x_i, x_j)\)를 알려주는 쿼리를 \((n + 25)\)번 이하로 사용하여 \(x_1..x_n\) 중 적어도 \((n-1)\)개의 값을 확정하여라. 즉,

  • 모든 \(i\)에 대해 \(y_i \le x_i\)
  • \(y_k \ne x_k\)인 \(k\)는 1개 이하

를 만족하는 어떤 수열 \(y_1..y_n\)을 찾아라.

접근

우선 처음 쿼리로 \(m = \min(x_a, x_b)\)를 알았다고 하자. 두 번째 쿼리부터 아래 과정을 반복한다.

  • 아직 쿼리를 해보지 않은 인덱스 \(c\)를 골라 ? a c 쿼리를 한다. \(r = \min(x_a, x_c)\)라 하자.
  • Case 1. \(r < m\)이라면, \(x_c = r\)이 확정된다.
  • Case 2. \(r > m\)이라면, \(x_b = m\)이 확정된다. \(b\)에 \(c\)를, \(m\)에 \(r\)을 대입한다.
  • Case 3. \(r = m\)이라면, \(x_a = m\)이 확정된다. \(a\)에 \(c\)를 대입한다. 이제 \(\min(x_a, x_b)\)을 모르니 ? a b를 추가로 수행하여 그 결과를 \(m\)에 대입한다.

위 과정이 한 번 완료될 때마다, 현재까지 본 수들 중 \(x_a, x_b\)만 제외하고 모두 값이 확정되어 있고, \(x_a, x_b\)는 현재까지 본 수들 중 가장 큰 2개라는 사실과 \(m = \min(x_a, x_b)\)을 알고 있는 상태가 유지된다.

그런데 Case 3은 쿼리를 1회가 아니라 2회 소모한다. 가령 수들의 값이 오름차순이 되도록 하는 순서로 인덱스 \(c\)를 고른다면 계속해서 Case 3에 걸리면서 쿼리 횟수가 \(2n\)에 육박하게 된다.

해결책은 인덱스 \(c\)를 선택하는 순서를 랜덤화하여 위험한 케이스들을 고확률로 회피하는 것이다. 랜덤 순서에 대해 실패 확률이 얼마나 되는지 측정해 보자. Case 3을 \(k\)번 만날 확률을 \(dp[n,k]\)라고 두면 다음 2차원 점화식이 성립한다.

\[dp[2,0] = 1 \\ dp[n,k] = \left(1 - \frac{2}{n}\right) dp[n-1,k] + \frac{2}{n} dp[n-1,k-1]\]

마지막에 선택하는 \(x_c\)가 가장 큰 수나 두 번째로 큰 수면 Case 3이 되고, 그렇지 않으면 Case 1이나 Case 2가 되기 때문이다.

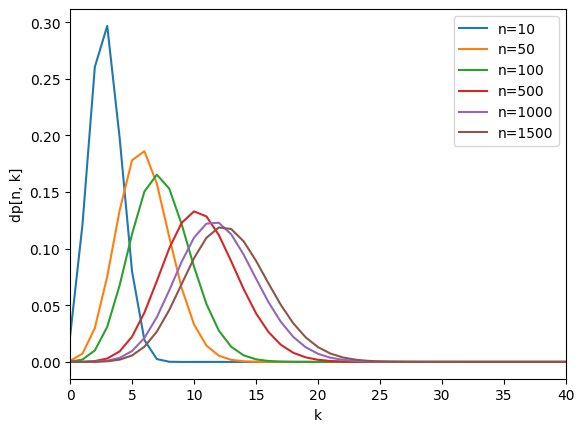
아래 플롯에서 보듯 문제가 요구하는 \(n\)의 범위에서 쿼리가 \((n+25)\)번 넘게 필요할 확률은 사실상 없다.

image

참고